The File system keeps a log each time some user performs a change folder operation. The operations are described below:

“../” : Move to the parent folder of the current folder. (If you are already in the main folder, remain in the same folder).
“./” : Remain in the same folder.
“x/” : Move to the child folder named x (This folder is guaranteed to always exist).

You are given a list of strings logs where logs[i] is the operation performed by the user at the ith step. The file system starts in the main folder, then the operations in logs are performed.

Return the minimum number of operations needed to go back to the main folder after the change folder operations.

Example 1:
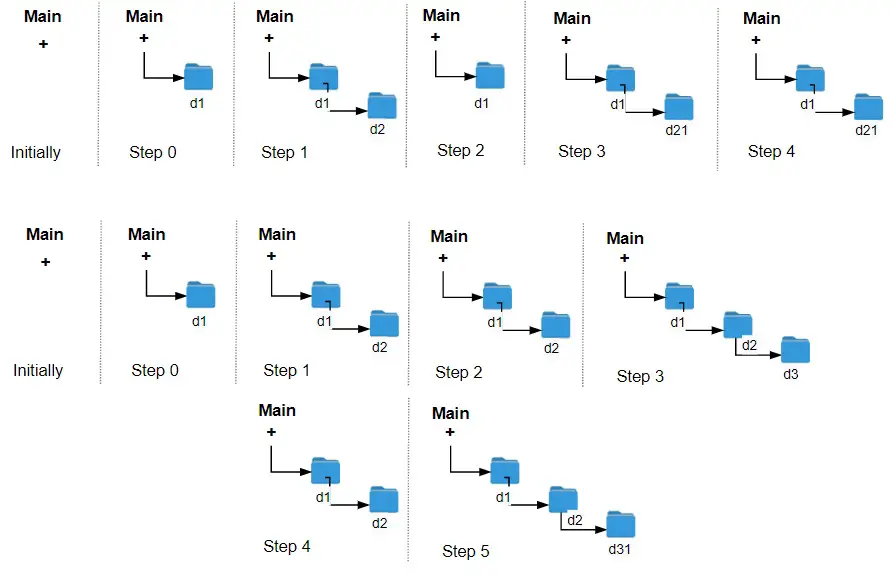
Input: logs = [“d1/”,”d2/”,”../”,”d21/”,”./”]
Output: 2
Explanation: Use this change folder operation “../” 2 times and go back to the main folder.

Example 2:
Input: logs = [“d1/”,”d2/”,”./”,”d3/”,”../”,”d31/”]
Output: 3

Example 3:
Input: logs = [“d1/”,”../”,”../”,”../”]
Output: 0

Constraints:
1 <= logs.length < 103
2 <= logs[i].length <= 10
logs[i] contains lowercase English letters, digits, ‘.’, and ‘/’.
logs[i] follows the format described in the statement.
Folder names consist of lowercase English letters and digits.

Hints:
Simulate the process but don’t move the pointer beyond the main folder.

Minimum Number of Operations to Crawl the Log Folder

The minimum operations would be to go up as many folders as we can until we reach the root. We can use a variable to remember which level of folder we are. And we can simulate the process but we need to make sure we do not move the depth above root.

1
2
3
4
5
6
7
8
9
10
11
12

class Solution {
public:
    int minOperations(vector<string>& logs) {
        int depth = 0;
        for (const auto &n: logs) {
            if (n == "../") {
                depth = max(0, depth - 1);
            } else if (n != "./") depth ++;
        }        
        return depth;
    }
};

class Solution {
public:
    int minOperations(vector<string>& logs) {
        int depth = 0;
        for (const auto &n: logs) {
            if (n == "../") {
                depth = max(0, depth - 1);
            } else if (n != "./") depth ++;
        }        
        return depth;
    }
};

The algorithm complexity is O(N). And the space requirement is O(1) constant.

–EOF (The Ultimate Computing & Technology Blog) —