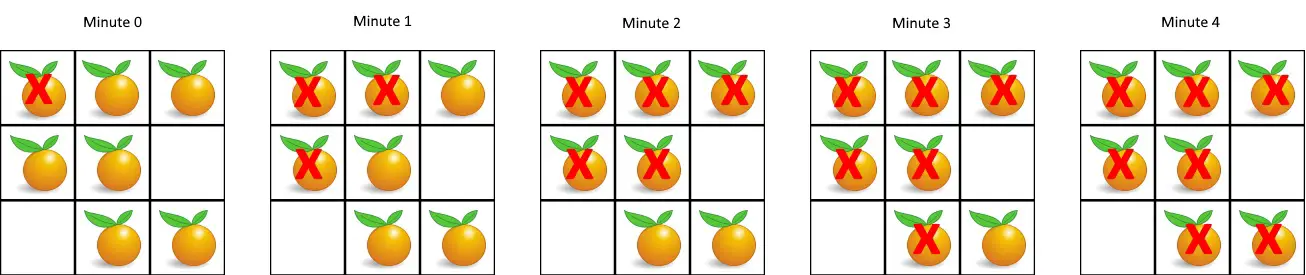
Breadth-First Search Algorithm to Solve Puzzle (Rotting Oranges)
- 时间:2020-09-24 11:41:27
- 分类:网络文摘
- 阅读:137 次
In a given grid, each cell can have one of three values:
the value 0 representing an empty cell;
the value 1 representing a fresh orange;
the value 2 representing a rotten orange.Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten. Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1 instead.
rotting-oranges-puzzle-using-bfs-algorithm
Input: [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Example 2:Input: [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:Input: [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.Note:
1 <= grid.length <= 10
1 <= grid[0].length <= 10
grid[i][j] is only 0, 1, or 2.
Breadth-First Search Algorithm to Solve Puzzle in a Grid
The Breadth First Search algorithm can be applied to multiple roots – which all indicate the same level. Thus, we push the initial rotten oranges into the queue – with minute equals to zero. When the queue is not empty, we pop up a node in the front of the queue, make a new node (its children with minute plus one and updated location), if the location is valid, it has a rotten orange on the cell, we increment the counter and push the child node to the queue.
The following C++ implements the Breadth First Search Algorithm, and tuples that consist of X, Y and minutes are pushed to the queue.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | class Solution { public: int orangesRotting(vector<vector<int>>& grid) { int row = grid.size(); if (row == 0) return 0; int col = grid[0].size(); int total = 0; queue<tuple<int, int, int>> Q; for (int i = 0; i < row; ++ i) { for (int j = 0; j < col; ++ j) { if (grid[i][j] == 2) { // push the initial rotten oranges to the queue Q.push(make_tuple(i, j, 0)); } else if (grid[i][j] == 1) { total ++; // fresh count } } } int step = 0, cnt = 0; // count to make a fresh rotten while (!Q.empty()) { auto p = Q.front(); Q.pop(); int r = std::get<0>(p); int c = std::get<1>(p); int s = std::get<2>(p); step = max(step, s); if ((r > 0) && (grid[r - 1][c] == 1)) { Q.push(make_tuple(r - 1, c, s + 1)); grid[r - 1][c] = 2; cnt ++; } if ((c > 0) && (grid[r][c - 1] == 1)) { Q.push(make_tuple(r, c - 1, s + 1)); grid[r][c - 1] = 2; cnt ++; } if ((r + 1 < row) && (grid[r + 1][c] == 1)) { Q.push(make_tuple(r + 1, c, s + 1)); grid[r + 1][c] = 2; cnt ++; } if ((c + 1 < col) && (grid[r][c + 1] == 1)) { Q.push(make_tuple(r, c + 1, s + 1)); grid[r][c + 1] = 2; cnt ++; } } return cnt == total ? step : -1; } }; |
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int row = grid.size();
if (row == 0) return 0;
int col = grid[0].size();
int total = 0;
queue<tuple<int, int, int>> Q;
for (int i = 0; i < row; ++ i) {
for (int j = 0; j < col; ++ j) {
if (grid[i][j] == 2) {
// push the initial rotten oranges to the queue
Q.push(make_tuple(i, j, 0));
} else if (grid[i][j] == 1) {
total ++; // fresh count
}
}
}
int step = 0, cnt = 0; // count to make a fresh rotten
while (!Q.empty()) {
auto p = Q.front();
Q.pop();
int r = std::get<0>(p);
int c = std::get<1>(p);
int s = std::get<2>(p);
step = max(step, s);
if ((r > 0) && (grid[r - 1][c] == 1)) {
Q.push(make_tuple(r - 1, c, s + 1));
grid[r - 1][c] = 2;
cnt ++;
}
if ((c > 0) && (grid[r][c - 1] == 1)) {
Q.push(make_tuple(r, c - 1, s + 1));
grid[r][c - 1] = 2;
cnt ++;
}
if ((r + 1 < row) && (grid[r + 1][c] == 1)) {
Q.push(make_tuple(r + 1, c, s + 1));
grid[r + 1][c] = 2;
cnt ++;
}
if ((c + 1 < col) && (grid[r][c + 1] == 1)) {
Q.push(make_tuple(r, c + 1, s + 1));
grid[r][c + 1] = 2;
cnt ++;
}
}
return cnt == total ? step : -1;
}
};The time complexity is O(N) where N is the number of the cells in the grid, and the space complexity is also O(N).
–EOF (The Ultimate Computing & Technology Blog) —
推荐阅读:梅文鼎与抽屉原理 人体上的尺子 一道行程问题 一道关于比的应用题 画家达·芬奇与数学 a与b成反比例,b与c成反比例,a与c成什么比例? 如何计算玻璃瓶(啤酒瓶)的容积 齿轮齿数比的问题 哪些类型的网站不适合使用虚拟主机? 针对网站安全防护 探讨waf防火墙的作用
- 评论列表
-
- 添加评论