How to Compute the Catalan Numbers using Dynamic Programming Alg
- 时间:2020-09-15 16:10:27
- 分类:网络文摘
- 阅读:129 次
Catalan numbers are popular in Combinatoric Mathematics. Many interesting counting problems tend to be solved using the Catalan numbers. The first few Catalan numbers are:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452
A few interesting Catalan counting problems:
- The number of different ways to cut a convex polygon into triangles i.e. n triangles – Catalan(n) ways
- The number of different ways i.e. Catalan(n) to form a full binary tree with n + 1 leaves
- The number of monotonic lattice paths (which do not pass above the diagonal) along the edges of a grid on a N x N square cells.
- Different ways to generate the parentheses: How to Generate Parentheses using Bruteforce or Depth First Search (Backtracking) Algorithms?
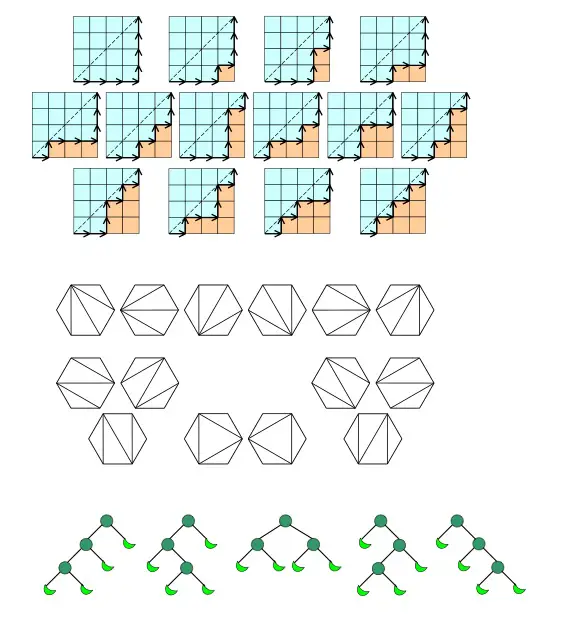
catalan-numbers-applications
Catalan Numbers Math Formula
The Catalan number can be computed in the simple form:
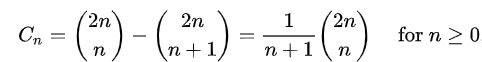
catalan-numbers-formula
There are several ways to compute the nth Catalan number. In order to compute the Catalan numbers in Dynamic Programming, we can use the following recurrence relation:
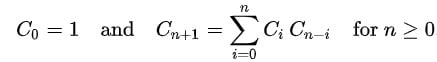
catalan-numbers-recurrence-relations
Alternatively, the following is a simple recurrence relation between Catalan number nth and nth+1.

catalan-numbers-recurrence-relations-simple
See this implementation based on the above simple Catalan formula: How to Compute the Catalan Number?
How to Compute the Catalan using Recursions?
The Catalan numbers grow quickly (exponentially) and will overflow if the N is large. The following is a naive implementation of the Catalan formula.
1 2 3 4 5 6 7 8 | int64_t catlan(int n) { if (n <= 1) return 1; int res = 0; for (int i = 0; i < n; i ++) { res += catlan(i) * catlan(n - i - 1); } return res; } |
int64_t catlan(int n) {
if (n <= 1) return 1;
int res = 0;
for (int i = 0; i < n; i ++) {
res += catlan(i) * catlan(n - i - 1);
}
return res;
}However, this implementation is not practically usable as the performance complexity is exponential. The intermediate catalan numbers are computed over and over again.
Dynamic Programming: Computing Catalan Numbers using Recursion + Memoization
We can improve the above recursive implementation into Dynamic Programming by simply using a hash map to store the intermediate calculations e.g. the Memoization.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | unordered_map<int, int64_t> memo; int64_t catlan(int n) { if (n <= 1) return 1; if (memo.find(n) != memo.end()) { // avoid duplicate calculations return memo[n]; } int res = 0; for (int i = 0; i < n; i ++) { res += catlan(i) * catlan(n - i - 1); } memo[n] = res; // store into the memo return res; } |
unordered_map<int, int64_t> memo;
int64_t catlan(int n) {
if (n <= 1) return 1;
if (memo.find(n) != memo.end()) {
// avoid duplicate calculations
return memo[n];
}
int res = 0;
for (int i = 0; i < n; i ++) {
res += catlan(i) * catlan(n - i - 1);
}
memo[n] = res; // store into the memo
return res;
}The intermediate calculations are computed and stored into the hash map for later retrieval. The overall time complexity is N square and the space requirement is O(N).
Dynamic Programming: Computing Catalan Numbers using Iterative Approach
Requiring a O(N) vector/array to store the Catalan numbers, we can do this purely iteratively in O(N^2) time complexity. This implementation eliminates the calling stacks due to recursion and is the most efficient (in terms of time and space) among the three implementations presented in this post.
1 2 3 4 5 6 7 8 9 10 11 | int catlan(int n) { vector<int64_t> dp(n + 1, 0); dp[0] = 1; dp[1] = 1; for (int i = 2; i <= n; i ++) { for (int j = 0; j < i; ++ j) { dp[i] += dp[j] * dp[i - j - 1]; } } return (int)dp.back(); } |
int catlan(int n) {
vector<int64_t> dp(n + 1, 0);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i ++) {
for (int j = 0; j < i; ++ j) {
dp[i] += dp[j] * dp[i - j - 1];
}
}
return (int)dp.back();
}You may be interested in this post: How to Compute the Catalan Number?
–EOF (The Ultimate Computing & Technology Blog) —
推荐阅读:Comparing Left and Right Branch of a Complete Binary Tree How to Find Words That Can Be Formed by Characters? How to Compute the Maximum Difference Between Node and Ancestor? How to Compute the Day of the Year? Blogger Mugged While Live-streaming Her Morning Commute Saudi Arabian Teen Arrested For Online Video Conversations With 8 Tips to Become An Expert Travel Blogger A Guide to Creating a Killer Social Media Marketing Strategy for Why Everyone Is Freaking Out Over This New WordPress Theme Million-Dollar Bloggers Share Their Secrets For Success
- 评论列表
-
- 添加评论